P8340 [AHOI2022] 山河重整

题面

解法

$20pts$ 给 $O(2^n)$ 枚举，$60pts$ 是 $O(n^2)$，先看看怎么做。计数题无非容斥和 $dp$，不妨从 $dp$ 入手。多项式复杂度的做法意味着无法将 $[1,n]$ 中是否能全部被表示直接存入状态，考虑将其转化为另一个充要条件，注意到：

$\forall i\in [1,n]$，需要满足 $S$ 中 $\le i$ 的元素之和 $\ge i$。

证明：必要性显然，考虑使用数学归纳法证明其必要性。$i=1,2$ 时显然，对于 $i \ge 3$，假设找到最小的 $x$ 使得 $\le x$ 的值相加的和 $\ge i$，设这个和为 $s$，则有 $s \lt 2i$（否则由于 $x \le i$ 则 $x$ 不是最小），而又有 $i \le s$，所以 $s - i \lt i$，由于 $\lt i$ 的可以被表示，所以 $\gt s - i$ 的也可以，即 $\ge i$ 的可以被表示，证毕。

于是进行 $O(n^2)$ 的背包 $dp$，可以获得 $60pts$，具体做法不再赘述。

然而这个状态不太好优化。思考完 $dp$，来考虑容斥（正难则反），即考虑不合法的情况有多少种。显然可以找到最小的 $x$ 使得 $S$ 中 $\le x$ 的元素之和 $\lt x$，将其方案数从总和内减去。又发现，若 $\le x$ 的元素之和 $\lt x$ 且 $x$ 最小，则 $\le x-1$ 的元素之和必定 $=x-1$。如此一来，不妨设 $f_i$ 为 $\le i$ 的元素之和为 $i$ 并且任意 $x \le i$ 都合法的方案数，状态数量被优化为线性。

那么，问题转化为如何快速求出 $fi$，同样可以容斥，用总方案数减去不合法的情况。总方案数就是 $i$ 的整数拆分方案数，这个后面会讲。而不合法的方案数就是全局不合法方案的一部分，可以通过 $f{1\cdots i-1}$ 计算出。

现在考虑对一个数 $n$ 进行整数拆分的方案数，一个 trivial 的想法是使用 $O(n^2)$ 的背包。注意到背包的第二维值域为 $n$，而由于每次第二维要加上 $i$，使得增长速度很快，所以只会进行 $\sqrt n$ 次第二维的增加操作，这给了我们优化的空间。

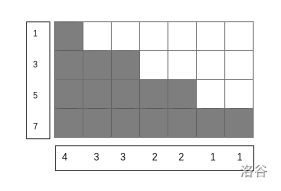
可以通过下图便于理解。行代表从小到大加入的不同的数，由于总方格数量为 $n$，所以行数是 $O(\sqrt n)$ 级别的。但如果按照一行一行地做就不免要枚举第一维加入的 $i$ 以及第二维的总和，复杂度是 $O(n^2)$。换一种思路，一列一列地做，相当于对 $[1,\sqrt{2n}] \cap \mathbb{Z}$ 做类似完全背包，并且为了保证每行互不相同，就需要让加入的数是连续的，只需要在 $dp$ 时多留心一下，就得到了 $O(n\sqrt n)$ 计算整数拆分的算法。

考虑前面的 $f_j$ 对后面 $f_i$ 的贡献，根据 $f_j$ 的定义，一定有 $j+1$ 没法被表示，所以 $j+(j+2) \le i$，同时要求 $[j+2,i]\cap S$ 的总和 $s+j=i$。类似于整数拆分，枚举新加入的列即可。如此一来，想要算出 $f_i$ 就要求前面的 $f_j$ 值已经确定。

考虑到 $j \le \frac{i}{2}$，可以通过类似于分治的方法，先计算出 $f{1\cdots n/2}$，然后在 $O(n \sqrt n)$ 的复杂度内贡献到 $f{n/2\cdots n}$ 中。总的时间复杂度为 $T(n) = O(n \sqrt n) + T(n / 2) = O(n \sqrt n)$。

AC代码

int n, p, pw2[MAXN], f[MAXN], g[MAXN];
inline void add(int& x, int y) { x += y, x >= p && (x -= p); }
void solve(int n) {
    if (n <= 1) return void(f[0] = 1);
    solve(n >> 1);
    for (int i = 0; i <= n; ++i) g[i] = 0;
    for (int i = sqrt(n * 2); i >= 1; --i) {
        for (int j = n; j >= i; --j) g[j] = g[j - i];
        for (int j = 0; j + (j + 2) * i <= n; ++j) add(g[j + (j + 2) * i], f[j]);
        for (int j = i; j <= n; ++j) add(g[j], g[j - i]);
    }
    for (int i = n / 2 + 1; i <= n; ++i) if (g[i]) add(f[i], p - g[i]);
}
signed main() {
    read(n), read(p), pw2[0] = 1;
    for (int i = 1; i <= n; ++i) pw2[i] = 2ll * pw2[i - 1] % p;
    for (int i = sqrt(n * 2); i >= 1; --i) {
        for (int j = n; j >= i; --j) f[j] = f[j - i];
        add(f[i], 1);
        for (int j = i; j <= n; ++j) add(f[j], f[j - i]);
    }
    solve(n);
    int ans = pw2[n];
    for (int i = 0; i < n; ++i)
        add(ans, p - (ll)f[i] * pw2[n - i - 1] % p);
    write(ans), putchar('\n');
    return 0;
}